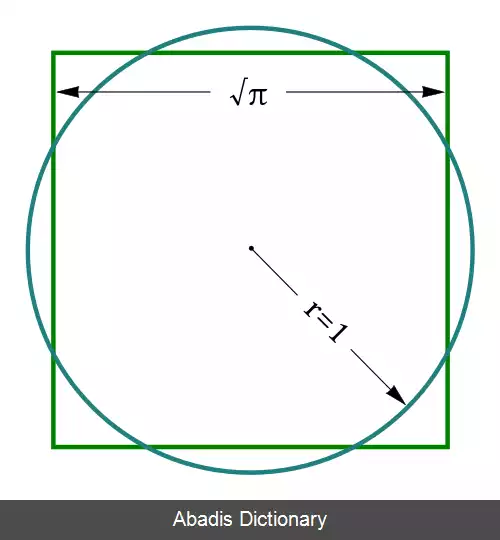
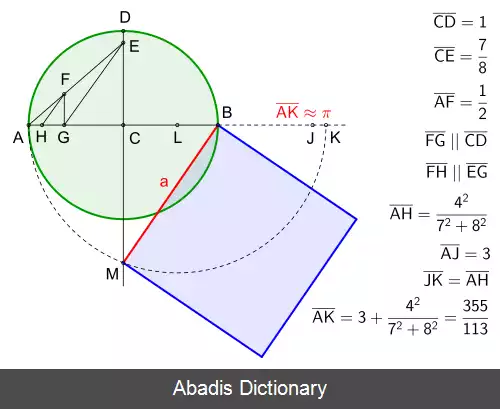
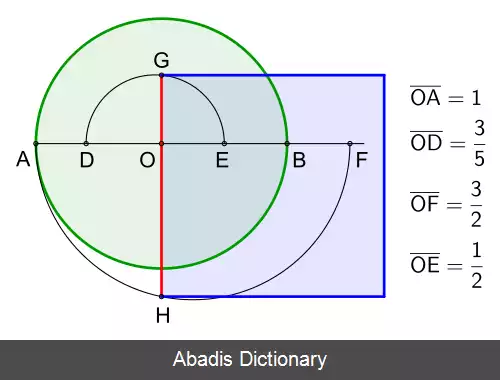
[ویکی فقه] تربیع دایره، مسئله ای در هندسه در باره ترسیم مربعی که مساحتش با مساحت دایره ای مفروض برابر باشد.
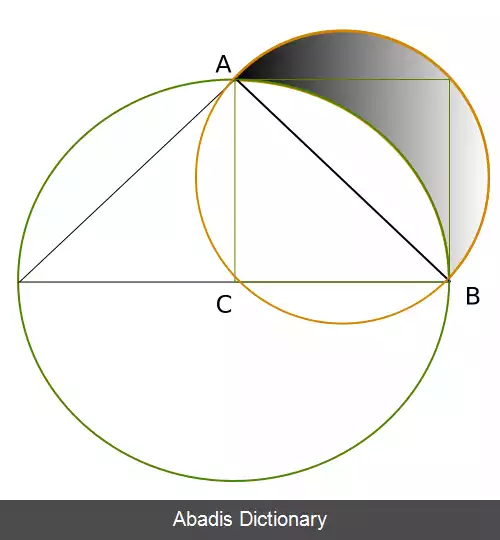
این مسئله، یکی از سه مسئله هندسی مشهور در یونان باستان و دوره اسلامی است (دو مسئله دیگر: تضعیف مکعب و تثلیث زاویه). اگر بتوان شکلی محصور با پاره خطهای راست یافت که مساحتش با مساحت دایره مفروض برابر باشد، این مسئله حل شدنی است.نسلهای متوالی از هندسه دانان یونان با این مسئله و گونه های مختلف آن درگیر بودند. در حدود ۴۵۰ ق م بقراط خیوسی نشان داد که به کمک خط کش و پرگار می توان مربعی هم مساحت با نوع خاصی ماهک (شکل هلالی محصور به دو کمان دایره) رسم کرد. او همچنین نشان داد که می توان مربعی یافت که مساحتش با نوعی دیگر از ماهک به علاوه یک دایره برابر باشد، البته این کار منجر به حل مسئلة تربیع دایره نمی شود. آنتیفونِ آتنی (ح ۴۰۰ ق م) متوجه شد که تربیع دایره به طور تقریبی ممکن است، زیرا می توان مربعهایی رسم کرد که مساحتشان با چند ضلعیهای منتظم محاطی دارای چهار یا هشت یا شانزده... ضلع برابر باشد. دینوستراتوس (میانة قرن چهارم پیش از میلاد ) برای تربیع دایره از یک منحنی غیرجبری به نام مربع ساز استفاده کرد. ارشمیدس (قرن سوم پیش از میلاد) ثابت کرد که مساحت دایره با مساحت مثلث قائم الزاویه ای که قاعده اش برابر با محیط دایره و ارتفاعش برابر با شعاع دایره باشد، برابر است؛ بنابراین، در صورتی که بتوان پاره خط راستی مساوی با محیط دایره رسم کرد، تربیع دایره ممکن است. ارشمیدس چنین پاره خطی را به کمک خط مماس بر یک مارپیچ رسم کرد. هیچیک از این راه حلها با ابزارهای متعارف در هندسة اقلیدسی ( خط کش و پرگار ) مقدور نیست و در واقع حل این مسئله با خط کش و پرگار ناممکن است. ارشمیدس روش دیگری هم برای حل این مسئله عرضه کرد که در نهایت مفیدتر از کار در آمد. او با در نظر گرفتن ۹۶ ضلعیهای منتظم محاطی و محیطی نشان داد که نسبت محیط دایره به قطر آن ــ که اکنون با حرف یونان نشان داده می شود ــ بتقریب ۱۷ ۳ ۱۰۷۱ ۳ است.
ریاضیدانان دوره اسلامی
ریاضیدانان دوره اسلامی نیز برای حل مسئله تربیع دایره، آن را از جنبة نظری و عملی یعنی بسط تقریبی و تکمیل روش دوم ارشمیدس ، بررسی کردند. دانشمندان دورة اسلامی نخستین بار از طریق رسالة تربیع الدائرة ارشمیدس که ثابت بن قُرّه آن را از یونانی به عربی ترجمه کرد، با مسئلة تربیع دایره آشنا شدند. این رساله در دورة اسلامی به نامهای تکسیر دایره ، مساحة الدایرة، و کتاب مساحة الدائرة و تکسیرها نیز شناخته می شد خواجه نصیرالدین طوسی در قرن هفتم آن را بازنویسی کرد. این بازنویسی با عنوان مقالة ارشمیدس فی تکسیر الدائرة در انتهای رسالة تحریر الکرة و الاسطوانة ارشمیدس به چاپ رسیده است. صفدی به اشتباه رساله ای با نام تربیع الدایرة را به خواجه نصیرالدین طوسی نسبت داده است و ون دایک نیز از متن چاپ شدة رسالة شکل القطاع خواجه نصیرالدین طوسی به اشتباه با عنوان تربیع الدائرة یاد کرده است.
← رساله ابن هیثم
تکلیف مسئلة تربیع دایره را سرانجام فردیناند لیندمان ، ریاضیدان آلمانی، در ۱۲۹۹/ ۱۸۸۲ با اثبات غیرجبری بودن عدد روشن کرد معنای حکم او این است که نمی تواند ریشة معادله ای جبری با ضریبهای صحیح باشد و بنابراین، مسئلة هندسیِ یافتنِ مربعی هم مساحت با دایرة مفروض نه با خط کش و پرگار حل شدنی است نه با سایر منحنیهای جبری مثل مقاطع مخروطی که در تثلیث زاویه و تضعیف مکعب به کار می روند. اثبات لیندمان بسیار پیچیده است، ولی بعدها نیون ، ریاضیدان انگلیسی (۱۲۵۹ـ ۱۳۳۵/ ۱۸۴۳ـ۱۹۱۷)، اثباتهای ساده تری یافت که برای هر دانشجوی ریاضی درک شدنی است. یانوش بویویی، ریاضیدان مجار (۱۲۱۷ـ۱۲۷۶/ ۱۸۰۲ـ۱۸۶۰)، در رساله اش درباره هندسة اقلیدسی با نام > پیوست (چاپ ۱۲۴۸/ ۱۸۳۲)، نشان داده است که تربیع دایره برای برخی دایره ها در هندسة نااقلیدسی ممکن است، زیرا مساحت این دایره ها برابر با ۲ است که در آن عدد متغیری وابسته به شعاع دایره است.
این مسئله، یکی از سه مسئله هندسی مشهور در یونان باستان و دوره اسلامی است (دو مسئله دیگر: تضعیف مکعب و تثلیث زاویه). اگر بتوان شکلی محصور با پاره خطهای راست یافت که مساحتش با مساحت دایره مفروض برابر باشد، این مسئله حل شدنی است.نسلهای متوالی از هندسه دانان یونان با این مسئله و گونه های مختلف آن درگیر بودند. در حدود ۴۵۰ ق م بقراط خیوسی نشان داد که به کمک خط کش و پرگار می توان مربعی هم مساحت با نوع خاصی ماهک (شکل هلالی محصور به دو کمان دایره) رسم کرد. او همچنین نشان داد که می توان مربعی یافت که مساحتش با نوعی دیگر از ماهک به علاوه یک دایره برابر باشد، البته این کار منجر به حل مسئلة تربیع دایره نمی شود. آنتیفونِ آتنی (ح ۴۰۰ ق م) متوجه شد که تربیع دایره به طور تقریبی ممکن است، زیرا می توان مربعهایی رسم کرد که مساحتشان با چند ضلعیهای منتظم محاطی دارای چهار یا هشت یا شانزده... ضلع برابر باشد. دینوستراتوس (میانة قرن چهارم پیش از میلاد ) برای تربیع دایره از یک منحنی غیرجبری به نام مربع ساز استفاده کرد. ارشمیدس (قرن سوم پیش از میلاد) ثابت کرد که مساحت دایره با مساحت مثلث قائم الزاویه ای که قاعده اش برابر با محیط دایره و ارتفاعش برابر با شعاع دایره باشد، برابر است؛ بنابراین، در صورتی که بتوان پاره خط راستی مساوی با محیط دایره رسم کرد، تربیع دایره ممکن است. ارشمیدس چنین پاره خطی را به کمک خط مماس بر یک مارپیچ رسم کرد. هیچیک از این راه حلها با ابزارهای متعارف در هندسة اقلیدسی ( خط کش و پرگار ) مقدور نیست و در واقع حل این مسئله با خط کش و پرگار ناممکن است. ارشمیدس روش دیگری هم برای حل این مسئله عرضه کرد که در نهایت مفیدتر از کار در آمد. او با در نظر گرفتن ۹۶ ضلعیهای منتظم محاطی و محیطی نشان داد که نسبت محیط دایره به قطر آن ــ که اکنون با حرف یونان نشان داده می شود ــ بتقریب ۱۷ ۳ ۱۰۷۱ ۳ است.
ریاضیدانان دوره اسلامی
ریاضیدانان دوره اسلامی نیز برای حل مسئله تربیع دایره، آن را از جنبة نظری و عملی یعنی بسط تقریبی و تکمیل روش دوم ارشمیدس ، بررسی کردند. دانشمندان دورة اسلامی نخستین بار از طریق رسالة تربیع الدائرة ارشمیدس که ثابت بن قُرّه آن را از یونانی به عربی ترجمه کرد، با مسئلة تربیع دایره آشنا شدند. این رساله در دورة اسلامی به نامهای تکسیر دایره ، مساحة الدایرة، و کتاب مساحة الدائرة و تکسیرها نیز شناخته می شد خواجه نصیرالدین طوسی در قرن هفتم آن را بازنویسی کرد. این بازنویسی با عنوان مقالة ارشمیدس فی تکسیر الدائرة در انتهای رسالة تحریر الکرة و الاسطوانة ارشمیدس به چاپ رسیده است. صفدی به اشتباه رساله ای با نام تربیع الدایرة را به خواجه نصیرالدین طوسی نسبت داده است و ون دایک نیز از متن چاپ شدة رسالة شکل القطاع خواجه نصیرالدین طوسی به اشتباه با عنوان تربیع الدائرة یاد کرده است.
← رساله ابن هیثم
تکلیف مسئلة تربیع دایره را سرانجام فردیناند لیندمان ، ریاضیدان آلمانی، در ۱۲۹۹/ ۱۸۸۲ با اثبات غیرجبری بودن عدد روشن کرد معنای حکم او این است که نمی تواند ریشة معادله ای جبری با ضریبهای صحیح باشد و بنابراین، مسئلة هندسیِ یافتنِ مربعی هم مساحت با دایرة مفروض نه با خط کش و پرگار حل شدنی است نه با سایر منحنیهای جبری مثل مقاطع مخروطی که در تثلیث زاویه و تضعیف مکعب به کار می روند. اثبات لیندمان بسیار پیچیده است، ولی بعدها نیون ، ریاضیدان انگلیسی (۱۲۵۹ـ ۱۳۳۵/ ۱۸۴۳ـ۱۹۱۷)، اثباتهای ساده تری یافت که برای هر دانشجوی ریاضی درک شدنی است. یانوش بویویی، ریاضیدان مجار (۱۲۱۷ـ۱۲۷۶/ ۱۸۰۲ـ۱۸۶۰)، در رساله اش درباره هندسة اقلیدسی با نام > پیوست (چاپ ۱۲۴۸/ ۱۸۳۲)، نشان داده است که تربیع دایره برای برخی دایره ها در هندسة نااقلیدسی ممکن است، زیرا مساحت این دایره ها برابر با ۲ است که در آن عدد متغیری وابسته به شعاع دایره است.
wikifeqh: تربیع_دایره