در نظریه اعداد، قضیه اعداد اول ( به انگلیسی: Prime Number Theorem ) ( PNT ) توزیع مجانبی اعداد اول بین اعداد صحیح مثبت را توصیف می کند. این قضیه ایده شهودی کم شدن چگالی اعداد اول در اعداد صحیح بزرگ را به صورت صوری و دقیق تر بیان می کند. قضیه اعداد اول به صورت مستقل و جداگانه توسط ژاک آدامار و چارلز پوسین در ۱۸۹۶ با استفاده از ایده های معرفی شده از سوی برنارد ریمان ( به خصوص تابع زتای ریمان ) اثبات شد.
اولین توزیع این چنینی که پیدا شد π ( N ) ∼ N l o g ( N ) بود که در آن π ( N ) تابع شمارنده تعداد اعداد اول و l o g ( N ) لگاریتم طبیعی عدد N است. بدین معنی که با بزرگ شدن N به میزان کافی، احتمال این که یک عدد صحیح تصادفی کوچک تر مساوی N اول باشد بسیار به 1 l o g ( N ) نزدیک است. بنابراین، احتمال اول بودن یک عدد صحیح با حداکثر 2 n رقم ( برای n های به اندازه کافی بزرگ ) حدوداً نصف عدد صحیح تصادفی با حداکثر n رقم است. به عنوان مثال، در میان اعداد صحیح مثبت با حداکثر ۱۰۰۰ رقم، حدود یک عدد از هر ۲۳۰۰ تا اول است ( l o g ( 10 1000 ) ≈ 2302. 6 ) ، درحالی که در میان اعداد صحیح با حداکثر ۲۰۰۰ رقم، حدود یکی از هر ۴۶۰۰ تا اول هستند ( l o g ( 10 2000 ) ≈ 4605. 2 ) . به بیان دیگر، میانگین شکاف بین اعداد اول پشت سر هم در میان N عدد صحیح ( از یک تا N ) حدود l o g ( N ) است. [ ۱]
اگر π ( x ) تعداد اعداد اول کمتر از x باشد
آن گاه
lim x → ∞ π ( x ) x / l n ( x ) = 1
با استفاده از قضیه اعداد اول می توان اثبات کرد که:
lim x → ∞ p ( x ) x ln ( x ) = 1
که در آن تابع p ( x ) ، تابع مولد اعداد اول باشد یعنی: x امین عدد اول p ( x ) =
می دانیم:
π ( x ) ∼ x ln x .
می دانیم توابع p ( x ) و π ( x ) معکوس هم هستند. یعنی:
p − 1 ( x ) = π ( x )
در نتیجه می توان با حل معادله π ( x ) = x تابع p ( x ) را یافت.
می دانیم π ( x ) ∼ x ln x .
پس با حل معادله x ln x = x می توان هم ارزی برای p ( x ) یافت.
به روش تکرار ساده معادله را حل می کنیم.
x 1 ln x = x 2
x 1 = x 2 ln ( x )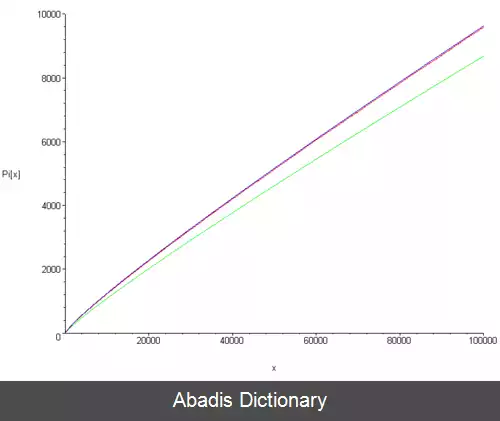
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاولین توزیع این چنینی که پیدا شد π ( N ) ∼ N l o g ( N ) بود که در آن π ( N ) تابع شمارنده تعداد اعداد اول و l o g ( N ) لگاریتم طبیعی عدد N است. بدین معنی که با بزرگ شدن N به میزان کافی، احتمال این که یک عدد صحیح تصادفی کوچک تر مساوی N اول باشد بسیار به 1 l o g ( N ) نزدیک است. بنابراین، احتمال اول بودن یک عدد صحیح با حداکثر 2 n رقم ( برای n های به اندازه کافی بزرگ ) حدوداً نصف عدد صحیح تصادفی با حداکثر n رقم است. به عنوان مثال، در میان اعداد صحیح مثبت با حداکثر ۱۰۰۰ رقم، حدود یک عدد از هر ۲۳۰۰ تا اول است ( l o g ( 10 1000 ) ≈ 2302. 6 ) ، درحالی که در میان اعداد صحیح با حداکثر ۲۰۰۰ رقم، حدود یکی از هر ۴۶۰۰ تا اول هستند ( l o g ( 10 2000 ) ≈ 4605. 2 ) . به بیان دیگر، میانگین شکاف بین اعداد اول پشت سر هم در میان N عدد صحیح ( از یک تا N ) حدود l o g ( N ) است. [ ۱]
اگر π ( x ) تعداد اعداد اول کمتر از x باشد
آن گاه
lim x → ∞ π ( x ) x / l n ( x ) = 1
با استفاده از قضیه اعداد اول می توان اثبات کرد که:
lim x → ∞ p ( x ) x ln ( x ) = 1
که در آن تابع p ( x ) ، تابع مولد اعداد اول باشد یعنی: x امین عدد اول p ( x ) =
می دانیم:
π ( x ) ∼ x ln x .
می دانیم توابع p ( x ) و π ( x ) معکوس هم هستند. یعنی:
p − 1 ( x ) = π ( x )
در نتیجه می توان با حل معادله π ( x ) = x تابع p ( x ) را یافت.
می دانیم π ( x ) ∼ x ln x .
پس با حل معادله x ln x = x می توان هم ارزی برای p ( x ) یافت.
به روش تکرار ساده معادله را حل می کنیم.
x 1 ln x = x 2
x 1 = x 2 ln ( x )

wiki: قضیه اعداد اول
