عدد گنگ
فرهنگستان زبان و ادب
دانشنامه عمومی
در ریاضیات، اعداد گنگ ( Irrational Numbers ) ، تمام اعداد حقیقی را شامل می شوند که گویا نباشند؛ یعنی، اعداد گنگ را نمی توان به صورت نسبت دو عدد صحیح نوشت. هنگامی که نسبت طول های دو پاره خط عددی گنگ باشد، آن پاره خط ها را می توان به عنوان «مقایسه ناپذیر» توصیف نمود، یعنی هیچ اندازه «مشترکی» ندارند، یا به عبارتی دیگر هیچ طولی ( یا «اندازه»ای ) ، هرچقدر هم کوچک باشد، وجود ندارد که بتوان از آن جهت بیان طول دو پاره خط مد نظر استفاده نمود، به گونه ای که آن پاره خط ها به صورت مضارب صحیحی از آن طول باشند.
برخی از اعداد گنگ شامل این مواردند: عدد π که نسبت محیط دایره به قطرش است، عدد اویلر e ، نسبت طلایی φ و ریشه مربعی ۲ ( ریشه دوم ۲ ) . [ ۱] [ ۲] [ ۳] درحقیقت، تمام ریشه های مربعی اعداد طبیعی به غیر از مربع های کامل، گنگ هستند.
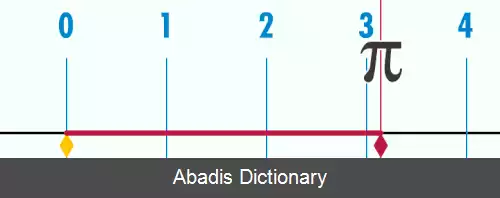
اعداد گنگ را همچون تمام اعداد حقیقی می توان برحسب ارزش مکانی ( مثلاً در دستگاه ده دهی ) بیان نمود. اعشار اعداد گنگ پایان ناپذیر است و دنباله متناوبی تشکیل نمی دهند. به عنوان مثال، نمایش ده دهی عدد π با ۳٫۱۴۱۵۹ شروع می شود، اما نمی توان با هیچ تعداد متناهی از ارقام، این عدد را نمایش داد و در ارقام اعشاری آن تکرار وجود ندارد. برعکس، بسط اعشاری که پایان پذیر بوده یا تناوب داشته باشد، لزوماً عدد گویایی است. این خواص اعداد گنگ و دستگاه ارزش مکانی را می توان اثبات نمود، با این حال از آن ها در ریاضیات به عنوان تعریف استفاده نمی شوند.
اعداد گنگ را به کمک کسرهای مسلسل پایان ناپذیر و بسیاری از طرق دیگر نیز می توان بیان نمود.
از اثبات کانتور در مورد ناشمارا بودن اعداد حقیقی و شمارا بودن اعداد گویا نتیجه می شود که تقریباً تمام اعداد حقیقی گنگ اند. [ ۴]
ابوکامل ریاضیدان مسلمان قرن نهم میلادی اولین کسی بود که در آثار خود اعداد گنگ را معرفی کرده و بکار برد. [ ۵]
شاید اولین عدد گنگی که بشر کشف کرد 2 بوده باشد. کشف این عدد منتسب به فیثاغورسیان ( شاگردان فیثاغورس ) است و گفته می شود در رقابت های علمی که در آن زمان بین گروه های مختلف در جریان بود این عدد نقش یک برگ برنده بزرگ را برای فیثاغورسیان ایفا می کرده است. این عدد طول قطر مربعی به ضلع واحد می باشد که به راحتی از رابطهٔ فیثاغورس a 2 + b 2 = c 2 بدست می آید. در ریاضیات کلاسیک هم 2 رایج ترین گزینه برای اثبات وجود اعداد گنگ است. در واقع ثابت می شود که عدد گویایی موجود نیست که مربع آن برابر با ۲ شود. اهمیت کشف اعداد گنگ در آنجا بود که نوعی عدم قطعیت به ریاضیات می داد؛ بدین معنا که برخلاف ذات ریاضیات یعنی قطعی بودن آن در عمل، اعداد گنگ را نمی توان به طور قطعی بیان کرد مثلاً بسط اعشاری همین عدد 2 نامختوم و نامتناوب است و برای نمایش آن مجبوریم به چند رقم اعشار آن اکتفا کنیم و بقیه را نادیده بگیریم، مثلاً می نویسیم: 2 = 1. 4142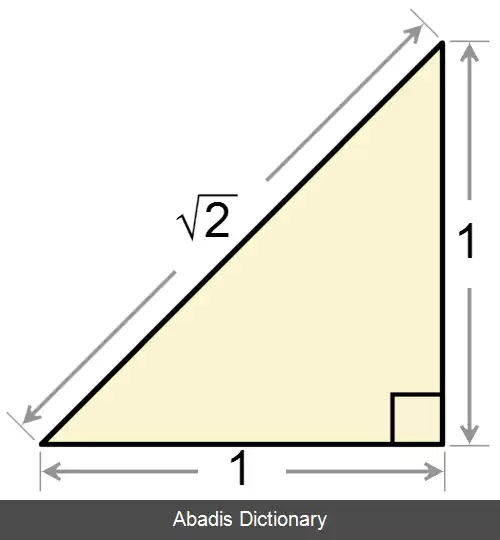
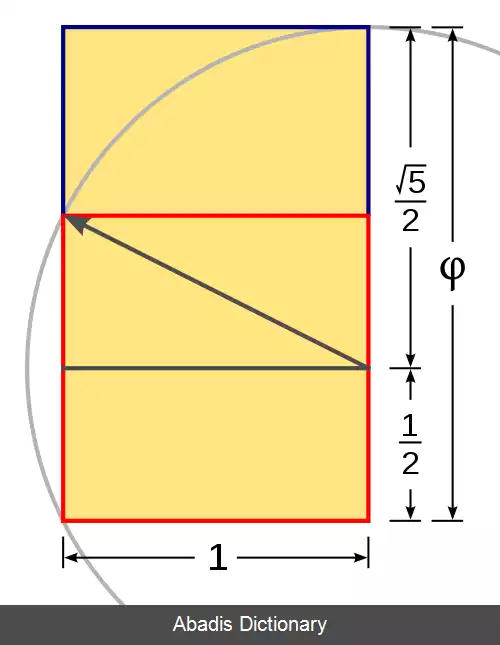
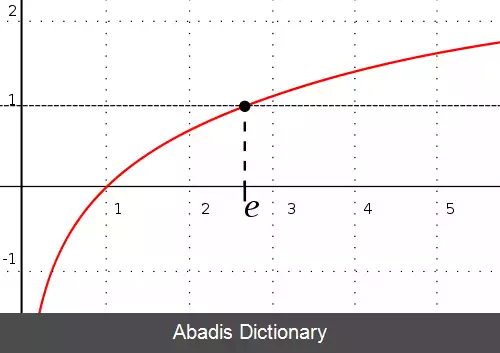
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرخی از اعداد گنگ شامل این مواردند: عدد π که نسبت محیط دایره به قطرش است، عدد اویلر e ، نسبت طلایی φ و ریشه مربعی ۲ ( ریشه دوم ۲ ) . [ ۱] [ ۲] [ ۳] درحقیقت، تمام ریشه های مربعی اعداد طبیعی به غیر از مربع های کامل، گنگ هستند.
اعداد گنگ را همچون تمام اعداد حقیقی می توان برحسب ارزش مکانی ( مثلاً در دستگاه ده دهی ) بیان نمود. اعشار اعداد گنگ پایان ناپذیر است و دنباله متناوبی تشکیل نمی دهند. به عنوان مثال، نمایش ده دهی عدد π با ۳٫۱۴۱۵۹ شروع می شود، اما نمی توان با هیچ تعداد متناهی از ارقام، این عدد را نمایش داد و در ارقام اعشاری آن تکرار وجود ندارد. برعکس، بسط اعشاری که پایان پذیر بوده یا تناوب داشته باشد، لزوماً عدد گویایی است. این خواص اعداد گنگ و دستگاه ارزش مکانی را می توان اثبات نمود، با این حال از آن ها در ریاضیات به عنوان تعریف استفاده نمی شوند.
اعداد گنگ را به کمک کسرهای مسلسل پایان ناپذیر و بسیاری از طرق دیگر نیز می توان بیان نمود.
از اثبات کانتور در مورد ناشمارا بودن اعداد حقیقی و شمارا بودن اعداد گویا نتیجه می شود که تقریباً تمام اعداد حقیقی گنگ اند. [ ۴]
ابوکامل ریاضیدان مسلمان قرن نهم میلادی اولین کسی بود که در آثار خود اعداد گنگ را معرفی کرده و بکار برد. [ ۵]
شاید اولین عدد گنگی که بشر کشف کرد 2 بوده باشد. کشف این عدد منتسب به فیثاغورسیان ( شاگردان فیثاغورس ) است و گفته می شود در رقابت های علمی که در آن زمان بین گروه های مختلف در جریان بود این عدد نقش یک برگ برنده بزرگ را برای فیثاغورسیان ایفا می کرده است. این عدد طول قطر مربعی به ضلع واحد می باشد که به راحتی از رابطهٔ فیثاغورس a 2 + b 2 = c 2 بدست می آید. در ریاضیات کلاسیک هم 2 رایج ترین گزینه برای اثبات وجود اعداد گنگ است. در واقع ثابت می شود که عدد گویایی موجود نیست که مربع آن برابر با ۲ شود. اهمیت کشف اعداد گنگ در آنجا بود که نوعی عدم قطعیت به ریاضیات می داد؛ بدین معنا که برخلاف ذات ریاضیات یعنی قطعی بودن آن در عمل، اعداد گنگ را نمی توان به طور قطعی بیان کرد مثلاً بسط اعشاری همین عدد 2 نامختوم و نامتناوب است و برای نمایش آن مجبوریم به چند رقم اعشار آن اکتفا کنیم و بقیه را نادیده بگیریم، مثلاً می نویسیم: 2 = 1. 4142





wiki: عدد گنگ
دانشنامه آزاد فارسی
عدد گُنْگ (irrational number)
عدد گُنْگ
(یا: عدد اصم) در ریاضیات، هر عددی که نتوان آن را به صورت کسری با صورت و مخرجی از جنس اعداد صحیح نمایش داد. بسیاری از ریشه های دوم اعداد، مانند (فرمول ۱)و نیز عددهای مهمی مانند π (نسبت محیط دایره به قطر آن، تقریباً برابر کسر اعشاری ۳.۱۴۱۵۹) و e (پایۀ لگاریتم طبیعی، تقریباً ۲.۷۱۸۲۸) اعداد گنگ اند.فرمول ۱:
اگر عدد گنگ را به صورت کسر اعشاری نشان دهند، سلسله ارقام بعد از ممیز آن هرگز پایان نمی پذیرد و دارای جزء مکرر، یعنی رقم یا دسته ای از ارقام که دایم تکرار شود، نیست. اعداد گنگ بر دو دسته اند: اعداد گنگ جبری که ریشه های معادلاتی چندجمله ای با ضرایب گویایند، و اعداد گنگ متعالی یا غیرجبری که ریشه های چنین معادلاتی نیستند. π و e جزء اعداد گنگ متعالی اند.
عدد گُنْگ
(یا: عدد اصم) در ریاضیات، هر عددی که نتوان آن را به صورت کسری با صورت و مخرجی از جنس اعداد صحیح نمایش داد. بسیاری از ریشه های دوم اعداد، مانند (فرمول ۱)و نیز عددهای مهمی مانند π (نسبت محیط دایره به قطر آن، تقریباً برابر کسر اعشاری ۳.۱۴۱۵۹) و e (پایۀ لگاریتم طبیعی، تقریباً ۲.۷۱۸۲۸) اعداد گنگ اند.فرمول ۱:
اگر عدد گنگ را به صورت کسر اعشاری نشان دهند، سلسله ارقام بعد از ممیز آن هرگز پایان نمی پذیرد و دارای جزء مکرر، یعنی رقم یا دسته ای از ارقام که دایم تکرار شود، نیست. اعداد گنگ بر دو دسته اند: اعداد گنگ جبری که ریشه های معادلاتی چندجمله ای با ضرایب گویایند، و اعداد گنگ متعالی یا غیرجبری که ریشه های چنین معادلاتی نیستند. π و e جزء اعداد گنگ متعالی اند.
wikijoo: عدد_گنگ
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
